Actividad 1

Enunciado

[S/07] Sea la función

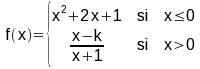
1. Calcule el valor de   k   para que la función   f   sea continua en   x = 0 . Para ese valor de   k , ¿es   f   derivable en   x =0 ?
2. Para   k = 0 , calcule las tendencias de  f ( x )   para   x → − ∞   y para   x → + ∞.

Recurso

Vamos a trabajar esta actividad con Geogebra.

Guía

Aquí algunas sugerencias:

1. En el campo de entrada introducimos un valor inicial para   k , luego las fórmulas de cada trozo y por último introducimos la definición de la función a trozos:
   k = 0
   p(x) = x² + 2 x + 1
   q(x) = ( x - k ) / ( x + 1)
   f(x) = Si [ x ≤ 0 , p(x) , q(x) ]
2. Hay demasiadas funciones representadas en la ventana gráfica ( p, q y f ). Dejaremos sólo   f . Para ello, en la ventana algebraica, pulsamos con el botón derecho tanto sobre   p   como sobre   q   y desmarcamos la opción Expone objeto.
3. veamos ya la segunda parte, pues tenemos   k = 0 . Los límites solicitadas podemos observarlos sin dificultad en la gráfica: ¿cuáles son las tendencias de la variable   y   cuando prolongamos hacia la izquierda ( x → − ∞ ) y hacia la derecha ( x → + ∞ ) indefinidamente?
4. Ahora pinchamos sobre   k   también en la ventana algebraica y movemos las flechas de dirección de nuestro teclado. De esa forma irá variando su valor y podremos observar cuándo la función es continua.
5. Se aprecia a simple vista que en ese caso el punto de conexión es anguloso. Pero podemos obtener las derivadas laterales en   x = 0   introduciendo en el campo de entrada:
   i = p'(0)
   d = q'(0)
6. Ahora escribimos en un cuadro de texto tres líneas: el valor de   k   para el que   f   es continua, si es o no derivable en ese valor y, por último, las tendencias solicitadas. Esto se puede ver en este pantallazo.
7. Guardamos el trabajo con el siguiente nombre: 04-actividad01.gbb

Actividad 2

Enunciado

[S/05] Halle   f ' ( 2 ) ,   g ' ( 4 )   y   h ' ( 0 )   para las funciones definidas de la siguiente forma:

Recurso

Vamos a trabajar esta actividad con Wiris. Cualquiera de los enlaces ofrecidos nos permitirá ejecutar Wiris en línea. Sería buena idea que abrieramos el enlace en una nueva pestaña.

• Wiris - Andalucía
• Wiris - Castilla y León
• Wiris - Catalunya
• Wiris - Madrid
• Wiris- UOC

Guía

Aquí algunas sugerencias:

1. En un bloque escribimos, como texto, el siguiente encabezado:
   Matemáticas Aplicadas a las CC.SS. II
   Cálculo de Derivadas
   Actividad 2
2. Insertamos un nuevo bloque y escribimos ahí las fórmulas de las funciones. Cada una en una línea. Puede sernos útil, para escribir paréntesis, fracciones y exponentes, las herramientas de la ficha Operaciones.
   f(x) := ...
   g(x) := ...
   h(x) := ...
3. Aunque no es estrictamente necesario, hallaremos las funciones derivadas. Para ello, en el mismo bloque, vamos escribiendo:
   f'(x)
   g'(x)
   h'(x)
4. Por fin, en tres nuevas líneas, colocamos ya los números solicititados:
   f'(x)
   g'(x)
   h'(x)
5. Tendremos algo como lo que puede verse en este pantallazo.
6. Ahora generamos el código html de nuestro trabajo yendo a Edición » Guardar y elegimos aquí la opción Obtener el código que añadiré a un html. Seleccionamos en el ratón el código de la ventana emergente, lo copiamos con Ctrl+C. Abrimos a continuación un editor de texto y pegamos en un documento el código copiado. Concluimos por fin guardando ese documento como un archivo de texto plano con este nombre: 04-actividad02.html

Actividad 3

Enunciado

[S/07] Sea la función definida para todo número real   x   por

f ( x ) = a x³ + b x

Determine   a   y   b   sabiendo que su gráfica pasa por el punto   A = ( 1 , 1 )   y que en ese punto la pendiente de la recta tangente es − 3 .

Recurso

Vamos a trabajar esta actividad con wxMaxima. Necesitaremos tener ese programa instalado en nuestro pc.

Guía

Aquí algunas sugerencias:

1. Definimos   f   y calculamos su derivada:
   f(x):= a*x^3-b*x
   diff(f(x),x)
   Esto último puede conseguirse mediante Análisis » Derivar...
2. Podemos llamar a la derivada obtenida   g(x). Eso puede hacerse copiando la fórmula y pegándola en el campo de entrada o escribiendo:
   g(x):= ''%
3. Las dos condiciones dadas en el enunciado equivalen a   f ( 1 ) = 1   y   g ( 1 ) = −3 .
4. Sólo queda resolver el sistema lineal formado por esas dos igualdades, donde las incógnitas son   a   y   b .
5. Esto último podemos conseguirlo así:
   - Vamos a Ecuaciones » Resolver sistema lineal
   - Elegimos el número de ecuaciones: 2.
   - Escribimos las ecuaciones: la primera   f ( 1 ) = 1   y la segunda   g ( 1 ) = −3 .
   - En el campo Variables indicamos las incógnitas, separadas por comas: a , b
6. Recordemos cómo se consigue directamente desde el campo de entrada:
   linsolve([ecuaciones separadas por comas],[incógnitas separadas por comas]).
7. Ahora con Editar » Insertar » Texto escribimos nuestras conclusiones, tal y como se puede ver en este pantallazo.
8. Guardamos el trabajo con el siguiente nombre: 04-actividad03.wxm