Actividad 1

Enunciado

Dadas siguientes matrices:

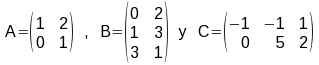
1. Obtengamos   X   con   A · X + B^t = 2 C .
2. Hallemos la matriz   Y   para que se verifica   A² − Y = C · B .
3. Razonemos si existe alguna matriz que conmute con   B .
4. Calculemos la matriz   A¹⁰⁰⁰ .

Recursos

Vamos a trabajar esta actividad con Wiris o con wxMaxima.

1. Cualquiera de los enlaces ofrecidos nos permitirá ejecutar Wiris en línea. Sería buena idea que abrieramos el enlace en una nueva pestaña.
   • Wiris - Andalucía
   • Wiris - Castilla y León
   • Wiris - Catalunya
   • Wiris - Madrid
   • Wiris- UOC
2. En cuanto a wxMaxima, necesitaremos tener ese programa instalado en nuestro sistema.

Guía para Wiris en línea

Aquí algunas sugerencias:

1. Podemos aprovechar cualquiera de los enlaces del ejemplo 1, que tenemos en la página dedicada a las ecuaciones matriciales.
2. En un bloque escribimos, como texto, el siguiente encabezado:
   Matemáticas Aplicadas a las CC.SS. II
   Matrices y Determinantes.
   Actividad 1
3. Insertamos un nuevo bloque y escribimos ahí las tres matrices, una en cada línea. Recuerda: Matrices » Matriz.
4. Dentro del mismo bloque, escribimos en una línea, cada una de las respuestas:
   Escribimos la expresión que resulta cuando despejamos   X   en el apartado a.
   Escribimos la operación que obtenemos cuando despejamos   Y   en el apartado b.
   Como comentario, el razonamiento que se pide en el apartado c.
   Obtenemos la potencia que se pide en el apartado d. Para el exponente tenemos Matrices » Potencia.
5. Ahora generamos el código html de nuestro trabajo yendo a Edición » Guardar y seleccionado ahora la opción Obtener el código que añadiré a un html. Seleccionamos en el ratón el código de la ventana emergente, lo copiamos con Ctrl+C. Abrimos a continuación un editor de texto y pegamos en un documento el código copiado. Concluimos por fin guardando ese documento como un archivo de texto plano con este nombre: 02-actividad01.html

Guía para wxMaxima

Aquí algunas sugerencias:

1. Puede resultarnos útil el estudio que hicimos en el ejemplo 2 de la página dedicada a las ecuaciones matriciales.
2. Abrimos el programa wxMaxima y procedemos así:
   - Introducimos las matrices
   - Escribimos la expresión que resulta cuando despejamos   X   en el apartado a.
   - Escribimos la operación que obtenemos cuando despejamos   Y   en el apartado b.
   - Escribimos, como texto, el razonamiento que se pide en el apartado c.
   - Calculamos   A¹⁰⁰⁰.
3. Comandos necesarios:
   Escribir la matriz   M : escribimos   M   en el campo de entrada y ahora vamos a Álgebra » Introducir matriz...
   Escribir texto: Editar » Insertar » Texto
   M^-1 : invert(M);
   M^t : transpose(M);
   Mⁿ : M^^n;
   
4. Guardamos el trabajo con el siguiente nombre: 02-actividad01.wxm

Actividad 2

Enunciado

Dado el sistema de ecuaciones lineales:

S : { 3 x − y + z = 7 , x + a y + z = 0 , 2 x − y + z = a + 3 }

1. Determinemos para qué valores de   a   la matriz   C   de coeficientes es inversible.
2. Obtengamos la inversa de   C   para   a = 0   y resolvamos   S   matricialmente
3. ¿Es compatible indeterminado el sistema para algún valor de  a ?

Recursos

Vamos a trabajar esta actividad con Wiris o con wxMaxima.

1. Cualquiera de los enlaces ofrecidos nos permitirá ejecutar Wiris en línea. Sería buena idea que abrieramos el enlace en una nueva pestaña.
   • Wiris - Andalucía
   • Wiris - Castilla y León
   • Wiris - Catalunya
   • Wiris - Madrid
   • Wiris- UOC
2. En cuanto a wxMaxima, necesitaremos tener ese programa instalado en nuestro sistema.

Guía para Wiris en línea

Aquí algunas sugerencias:

1. Podemos aprovechar cualquiera de los enlaces del ejemplo 1, que tenemos en la página dedicada a los sistemas de ecuaciones.
2. En un bloque escribimos, como texto, el siguiente encabezado:
   Matemáticas Aplicadas a las CC.SS. II
   Matrices y Determinantes.
   Actividad 2
3. Insertamos un nuevo bloque y escribimos ahí la matriz   C   de coeficientes y la matriz   B   de términos independientes, cada una en una línea. Recuerda: Matrices » Matriz.
4. Dentro del mismo bloque desarrollamos:
   Calculamos el determinante de   C .
   Resolvemos la ecuación   | C | = 0 : para esos valores la matriz no tiene inversa.
   Ponemos   a = 0   y despejamos   X   de   C · X = B .
   Deducimos de la Regla de Cramer, que sólo podrá ser compatible indeterminado cuando   | C | = 0 . Resolvamos el sistema para el valor de   a   en que esto ocurre y veamos cómo sale el sistema.
   
5. Ahora generamos el código html de nuestro trabajo yendo a Edición » Guardar y seleccionado ahora la opción Obtener el código que añadiré a un html. Seleccionamos en el ratón el código de la ventana emergente, lo copiamos con Ctrl+C. Abrimos a continuación un editor de texto y pegamos en un documento el código copiado. Concluimos por fin guardando ese documento como un archivo de texto plano con este nombre: 02-actividad02.html

Guía para wxMaxima

Aquí algunas sugerencias:

1. Puede resultarnos útil el estudio que hicimos en el ejemplo 2 de la página dedicada a los sistemas de ecuaciones lineales.
2. Abrimos el programa wxMaxima y procedemos así:
   Escribamos las matrices   C   de coeficientes y   B   de términos independientes.
   Calculamos el determinante de   C .
   Igualamos a cero el determinante de   C : en ese caso la matriz no tiene inversa.
   Despejamos   X   de   C · X = B   con   a = 0 .
   Deducimos de la Regla de Cramer, que sólo podrá ser compatible indeterminado cuando el determinante de   C   es cero. Resolvamos el sistema para el valor de   a   en que esto ocurre, así veremos cómo es.
   
3. Comandos necesarios:
   Escribir la matriz   M : escribimos   M   en el campo de entrada y ahora vamos a Álgebra » Introducir matriz...
   Escribir texto: Editar » Insertar » Texto
   M^-1 : invert(M);
   determinante de   M : determinant ( M ) ;
   resolver una ecuación: solve ( ecuación , [incógnita] ) ;
4. Guardamos el trabajo con el siguiente nombre: 02-actividad02.wxm