Processing math: 100%

Límites y Continuidad de Funciones

Matemáticas I

Límites y Continuidad de Funciones - Actividades

En este bloque se propone la realización de unas actividades. Se trata de unos ejercicios, problemas o cuestiones. Contaremos con la ayuda de los recursos señalados en cada una o con una resolución guiada.

Una vez concluida la actividad que estemos realizando, procederemos según se indica en cada una de ellas. Posteriormente podremos entregarla o compartirla siguiendo el procedimiento convenido para tal fin.

Actividad 1

Datos

Consideremos las funciones f y g definidas como siguen:

f(x)={x2+4xsix≤1x−2six>1,g(x)={x+1six≤12x2+xsix>1

Así como la función h cuya gráfica se muestra:

Gráfica de la función h

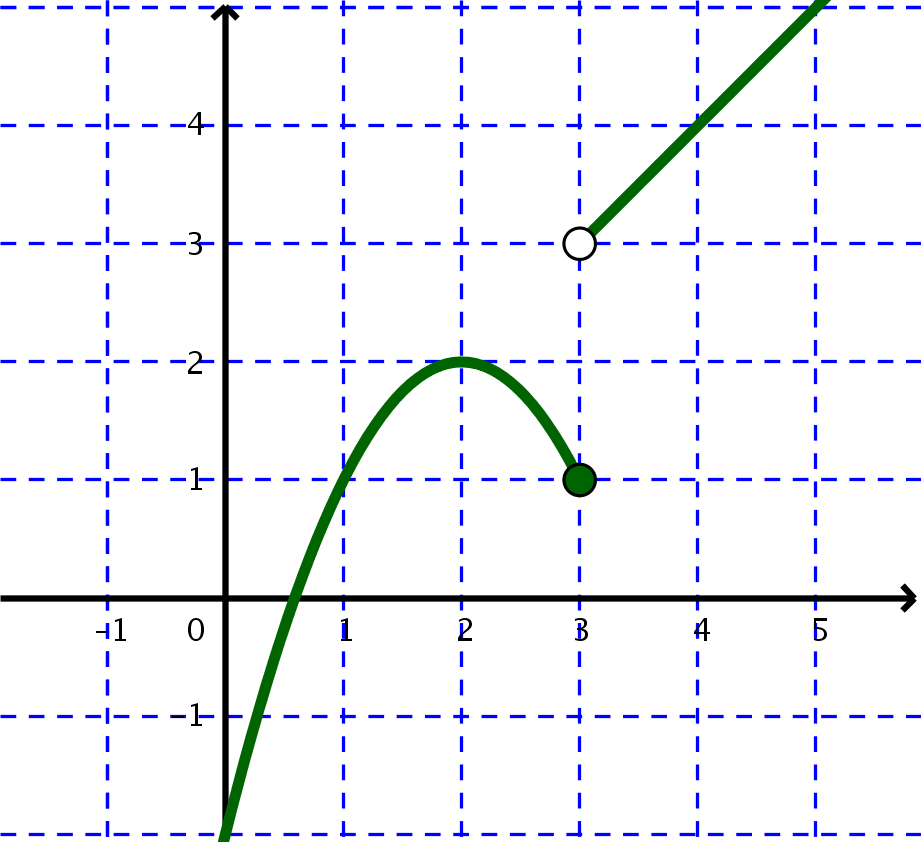
Recursos

Los ejemplos de las páginas 4 y 5 del texto de la lección.

Cuestionario

Completemos el esbozo que sigue:

  1. La función f sólo puede ser discontinua para x = . En este punto:
    • El valor es f(1) =
    • El límite por la izquierda es f(1−) =
    • El límite por la izquierda es f(1+) =
  2. Por ello ahí f es  
  3. La función g sólo puede ser discontinua para x = . En este punto:
    • El valor es g(1) =
    • El límite por la izquierda es g(1−) =
    • El límite por la izquierda es g(1+) =
  4. Por ello ahí g es  
  5. En la gráfica vemos que h para x=2 es  
  6. Y en la gráfica de h para x=3 apreciamos que son
    • h(3) =
    • h(3−) =
    • h(3+) =
  7. Por ello ahí h es
    continua
    discontinua evitable
    discontinua de salto

Cuando pulsemos sobre Enviar se generará una página que recogerá nuestas respuestas y elecciones.

 

Actividad 2

Datos

Consideremos la función f definida como sigue:

f(x)=3x−3x2−x

Recursos

Último ejemplo de la página 6 del texto de la lección.

Cuestionario

Completemos el esbozo que sigue:

  1. Los ceros del denominador, ordenados de menor a mayor, son: x = , x = .
  2. Por ello f para dichos valores:  
  3. Para todos los valores distintos de los anteriores la función es
    no lo sé
    continua
    discontinua evitable
    discontinua de salto finito
    discontinua de salto infinito
  4. Estudiemos la continuidad para x=0
    1. Para x=0 el denominador es cero, por ello en ese punto el valor es  
    2. Al calcular el límite de f(x) para x→0 obtenemos: limx→03x−3x2−x=−30 por ello ese límite es  
    3. Para averiguar el signo en el anterior sustituimos x=−0.001 obteniendo f(0−)=   y x=+0.001 obteniendo f(0+)=  
    4. De lo anterior deducimos que f para x=0 es
      continua
      discontinua evitable
      discontinua de salto finito
      discontinua de salto infinito
  5. Estudiemos la continuidad para x=1
    1. Para x=1 el denominador es cero, por ello en ese punto el valor es  
    2. Al calcular el límite de f(x) para x→1 obtenemos: limx→13x−3x2−x=00 por ello ese límite es  
    3. Y entonces hemos de   . Al hacerlo y volver a tomar límite obtenemos  
    4. De lo anterior deducimos que f para x=1 es
      continua
      discontinua evitable
      discontinua de salto finito
      discontinua de salto infinito

Cuando pulsemos sobre Enviar se generará una página que recogerá nuestas respuestas y elecciones.

 

Actividad 3

Datos

Consideremos la función f cuya gráfica es la siguiente:

Gráfica de la función f

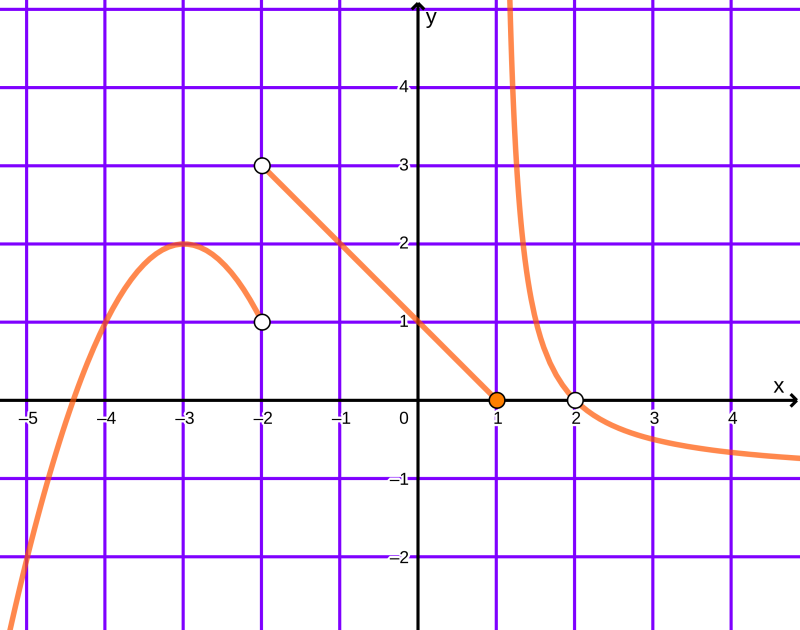
Recursos

Ejercicio 1 de la Autoevaluación del texto de la lección así como los vídeo 4 y el vídeo 5 que ya vimos en su día.

Cuestionario

Completemos el esbozo que sigue (copia y pega " ∅ " para " no existe " y " ∞ " para " infinito "):

  1. La función sólo es discontinua para las tres abscisas siguientes, ordenadas de menor a mayor:

    a = , b = , c =

  2. Para x=a la función es  , siendo valor y límites:
    • f(a)=
    • f(a−)=
    • f(a+)=
  3. Para x=b la función es  , siendo valor y límites:
    • f(b)=
    • f(b−)=
    • f(b+)=
  4. Para x=c la función es  , siendo valor y límites:
    • f(c)=
    • f(c−)=
    • f(c+)=
  5. Y los límites de prolongación son:
    • f(−∞)=
    • f(+∞)=
  6. En cuanto a sus asíntotas:
    • La asíntota vertical de f es =
    • La asíntota horizontal de f es =

Cuando pulsemos sobre Enviar se generará una página que recogerá nuestas respuestas y elecciones.