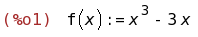
(%i1)
f(x):= x^3-3*x;
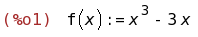
(%i2)
limit(f(x), x, minf);
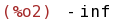
(%i3)
limit(f(x), x, inf);
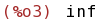
(%i4)
diff(f(x), x);
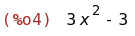
(%i5)
g(x):=3*x^2-3;
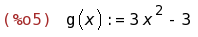
(%i6)
solve(g(x), [x]);
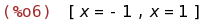
(%i7)
g(-2); g(0) ; g(2);

(%i10)
solve(f(x), [x]);
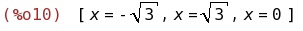
(%i11)
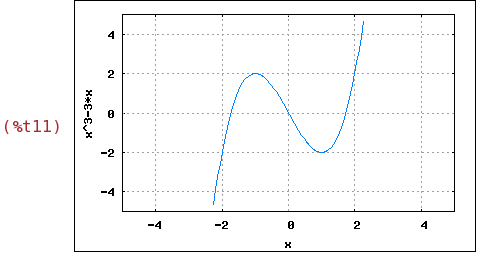
wxplot2d([f(x)], [x,-5,5], [y,-5,5],
[gnuplot_preamble, "set grid;"])$
(%i12)
plot2d([f(x)], [x,-5,5], [y,-5,5],
[plot_format, gnuplot],
[gnuplot_preamble, "set grid;"],
[nticks,1])$
(%i13)
- Su dominio es el conjunto de todos los reales y es continua en todo punto.
- No tiene asíntotas de ningún tipo (a no ser que ella misma sea una recta)
- Sólo tendremos que hallar los límites en el infinito, estudiar la monotonía y averiguar los extremos.
- Opcionalmente: cortes con los ejes y curvatura (concavidad, convexidad e inflexiones).
Nosotros haremos lo siguiente:
(%i01) Aquí introduciremos la fórmula de la función.
(%i02) Calcularemos el límite en menos infinito. Puede hacerse con Análisis-> Calcular límite.
(%i03) Calcularemos el límite en más infinito.
(%i04) Hallaremos la derivada. Puede hacerse con Análisis -> Derivar, colocando en la expresión f(x).
(%i05) Hemos llamado g(x) a la función derivada.
(%i06) Veremos los ceros de la derivada. Puede hacerse con Ecuaciones -> Resolver.
(%i07) Sustituiremos algunos valores en la derivada para conocer los intervalos de signo.
(%i10) Hallaremos los ceros: cortes con el eje X (opcional).
Ya dibujaremos la gráfica:
(%i11) Pasamos a dibujar la función en línea. Para ello vamos a Gráficos -> 2D
Expresión: f(x)
Intervalos para x e y: de -5 a 5.
Formato: en línea.
(%i12) Ahora la dibujaremos en gnuplot.Para ello vamos a Gráficos -> 2D
Expresión: f(x)
Intervalos para x e y: de -5 a 5.
Formato: gnulot.