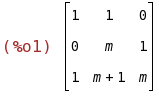
(%i1)
C:matrix([1,1,0],[0,m,1],[1,m+1,m]);
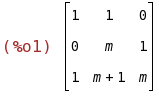
(%i2)
X:matrix([x],[y],[z]);
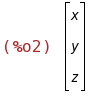
(%i3)
B:matrix([1],[0],[m+1]);
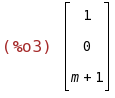
(%i4)
determinant(C);
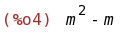
(%i5)
solve(determinant(C)=0);
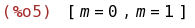
(%i6)
linsolve([x+y=1,z=0,x+y=1],[x,y,z]);
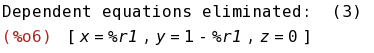
(%i7)
linsolve([x+y=1,y+z=0,x+2*y+z=2],[x,y,z]);

(%i8)
linsolve([x+y=1,m*y+z=0,x + (m+1)*y+m*z=m+1],[x,y,z]);
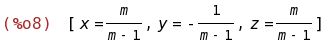
(%i9)
- Todo sistema de ecuaciones lineales puede expresarse como una ecuación matricial: C.X=B
C es la matriz de coeficientes
X es la matriz columna de las incógnitas
B la matriz columna de los términos independientes.
- Si C es cuadrada con determinante no nulo, podemos resolver matricialmente: C.X=B -> X=invert(C).B
- De ahí se deduce la llamada "Regla de Cramer para un sistema S(nxn):
1. Si determinant(C) no es cero es S compatible determinado.
2. Es x(i) = determinant(C(i)) / determinant(C)
donde C(i) es la matriz obtenida al sustituir por B la columna i de C.
- Así, un sistema S(nxn) sólo puede ser incompatible o compatible indeterminado cuando determinant(C)=0.