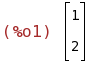
(%i1)
A:matrix([1],[2]);
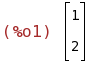
(%i2)
B:matrix([1,2],[3,5]);
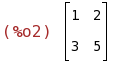
(%i3)
C:matrix([1,0,-1],[0,m,-6],[1,1,-m]);
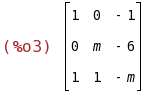
(%i4)
invert(A);

(%i5)
invert(B);
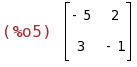
(%i6)
determinant(B); adjoint(B);
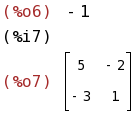
(%i8)
1/determinant(B) * adjoint(B);
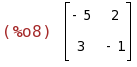
(%i9)
solve(determinant(C)=0);
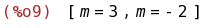
(%i10)
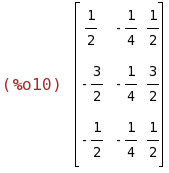
invert(C),m=2;
(%i11)
- Sólo las matrices cuadradas tienen inversa.
- Dos matrices se dice que son inversas cuando su producto es la matriz unidad o identidad.
- No todas las matrices cuadradas tienen inversa.
- Una matriz cuadrada tiene inversa precisamente cuando su determinante no es cero.
- En ese caso, la inversa es igual al inverso del determinante por la traspuesta de la adjunta.
CÓMO:
- Para calcular una inversa en wxMaxima podemos proceder así:
1. Escribimos la matriz, colocándole un nombre. Digamos A.
2. A continuación escribimos en el campo de entrada invert(A).
3. También podemos
a. Escribir en el campo de entrada A
b. Vamos a Álgebra -> Invertir matriz.
TRASPUESTA DE LA MATRIZ DE ADJUNTOS:
- Con wxMaxima también podemos calcular directamente esa matriz:
1. Escribimos la matriz, colocándole un nombre. Digamos A.
2. A continuación escribimos en el campo de entrada adjoint(A).
3. También podemos
a. Escribir en el campo de entrada A
b. Vamos a Álgebra -> Matriz adjunta.
- ¡Cuidado! Algunos autores denominan directamente matriz adjunta a la matriz de adjuntos o cofactores.