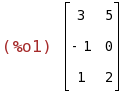
(%i1)
A:matrix([3,5],[-1,0],[1,2]);
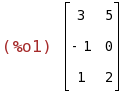
(%i2)
B:matrix([-1,3]); C:matrix([1],[-1],[0]);
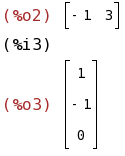
(%i4)
D:matrix([3,0],[-1,4]); O:matrix([0,0],[0,0]);

(%i6)
transpose(A);
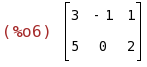
(%i7)
A[1,2];
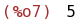
(%i8)
- Una matriz es una tabla numérica: un conjunto de números ordenados en filas y columnas.
- Se colocan entre paréntesis o corchetes se designa con una letra mayúscula: A, B, C,...
CÓMO:
- Para escribir una matriz en wxMaxima:
1. Escribimos en el campo de entrada el nombre seguido de dos puntos.
2. Vamos a Álgebra -> Introducir matriz.
3. Elegimos las dimensiones.
4. Completamos con los números.
- Si dominamos Maxima podemos hacerlo directamente en el campo de entrada:
M = matrix ( [fila 1] , [fila 2] , ... , [fila n] )
donde los elementos de cada fila van separados por comas.
TRASPUESTA
- La traspuesta de M es la matriz que se obtiene intercambiando sus filas por sus columnas.
- Para hallar la traspuesta de una matriz:
1. Escribimos su nombre en el campo de entrada.
2. Vamos a: Álgebra -> Transponer matriz.
- Si dominamos Maxima, basta escribir en el campo de entrada, directamente:
Transpose(M)
para que calcule la transpuesta de M.