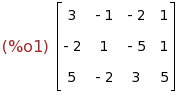
(%i1)
A: matrix([3,-1,-2,1],[-2,1,-5,1],[5,-2,3,5]);
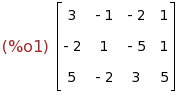
(%i2)
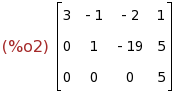
triangularize(A);
(%i3)
kill(all);
(%i1)
A: matrix([4,-1,-1,1],[-9,2,3,-1],[-5,1,2,0]);
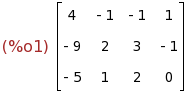
(%i2)
triangularize(A);
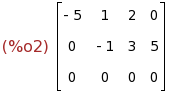
(%i3)
z:t $ solve(-y+3*z=5,[y]);
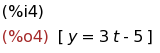
(%i5)
z:t $ y:3*t-5 $ solve(-5*x+y+2*z=0,[x]);
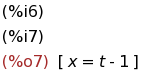
(%i8)
kill(all);
(%i1)
A: matrix([2,1,-3,1],[-1,5,2,3],[-2,5,-2,5]);
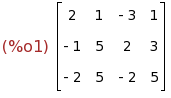
(%i2)
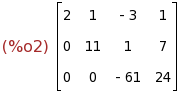
triangularize(A);
(%i3)
solve(-61*z=24);
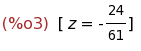
(%i4)
z : -24/61 $ solve(11*y+z=7,[y]);
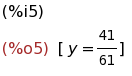
(%i6)
z : -24/61 $ y : 41/61 $ solve(2*x+y-3*z=1,[x]);
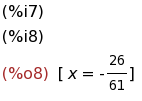
(%i9)
- Vamos a Álgebra -> Introducir matriz y escribimos la matriz del sistema.
- Ahora 'escalonamos' esa matriz escribiendo en la entrada: triangularize.
- Ahora nos corresponde interpretar el resultado.
- Podemos resolver manualmente el sistema si lo deseamos.
A veces conviene borrar variables, valores,... para no mezclar cálculos:
- Vamos a Maxima -> Limpiar memoria, o lo que es igual, ejecutamos: kill(all).